Gaußfunktion fitten mit lsqcurvefit

WICHTIG: Der Betrieb von goMatlab.de wird privat finanziert fortgesetzt. - Mehr Infos...

Partner:

Forum

Option

[Erweitert]

• Diese Seite per Mail weiterempfehlen

Gehe zu:

SaFW

Themenstarter

Forum-Anfänger


	Beiträge: 12

	Anmeldedatum: 24.02.20

	Wohnort: ---

	Version: ---

Verfasst am: 23.03.2020, 17:43 Titel:

Hallo,

gut, dann hier nochmal alles vollständig.
Also hier ist mein Versuch die Daten zu normieren und daraus dann einen ordentlichen Plot zu bekommen

Code:

Daten= [3 24 4 11 18 6 12 7 16 3 28 8 6 9 25 26 20 8 34 30 35 17 30 21 26 29 27 57 58 51 62 57 76 65 76 104 87 99 108 112 117 127 174 147 155 166 185 213 208 206 238 224 255 232 232 255 255 254 255 255 255 255 255 255 255 255 255 255 226 215 235 238 211 172 208 188 181 151 143 129 132 116 119 112 93 96 99 66 68 53 65 43 64 30 51 26 33 41 23 25 15 25 27 23 24 26 20 11 10 23 17 10 4 14 23 20 2 25 3 14 11]; % in uint8
Daten_normiert = Daten ./ max(max(Daten));
ydata = double(Daten_normiert);
xdata = 1:length(Daten_normiert);
plot(xdata,ydata);
hold on
mu = mean(ydata);
sig = std(ydata);
x=[mu sig];
F=lsqcurvefit(@Gauss,x,xdata,ydata);
yFitted = Gauss(F, xdata);
plot(xdata, yFitted)

Funktion ohne Link?

Das Ergebnis ist im ersten Bild zu sehen... Confused

Anschließend habe ich versucht die Fit-Daten zu skalieren. Dabei bin ich aber erstmal auf die Frage gestoßen, was denn am sinnvollsten wäre. Dachte mir also, dass eine Exponentialfunktion vielleicht sinnvoll wäre. Habe es also damit versucht

Code:

xdata = 1:length(Daten);
ydata = double(Daten);
plot(xdata,ydata);
hold on
mu = mean(ydata);
sig = std(ydata);
x=[mu sig];
F=lsqcurvefit(@Gauss,x,xdata,ydata);
yFit = Gauss(F, xdata);
plot(xdata,F(1)*exp(F(2)*yFit.^2))

Funktion ohne Link?

Das Ergebnis ist auch nicht zufriedenstellend. (siehe zweites Bild)
Hab jetzt keine weiteren Ideen wie ich das lösen kann und das es so aussieht wie im letzten Bild.
Kann es sein, dass ich noch die Amplitude mit in meine Rechnung mit einbeziehen muss?

Gruß

Lösung.png

Beschreibung:

die erhoffte Lösung

Download

Dateiname:

Lösung.png

Dateigröße:

46.89 KB

Heruntergeladen:

237 mal

Graph4.png

Beschreibung:

Skalierung

Download

Dateiname:

Graph4.png

Dateigröße:

11.18 KB

Heruntergeladen:

253 mal

Graph3.png

Beschreibung:

Normierung

Download

Dateiname:

Graph3.png

Dateigröße:

14.16 KB

Heruntergeladen:

233 mal

Harald

Forum-Meister


	Beiträge: 24.495

	Anmeldedatum: 26.03.09

	Wohnort: Nähe München

	Version: ab 2017b

Verfasst am: 23.03.2020, 18:08 Titel:

Hallo,

die Skalierung war nicht sinnvoll. So wird ja nicht die Fläche 1. Dann waren auch die Startwerte noch ein Problem.

Code:

Daten= [3 24 4 11 18 6 12 7 16 3 28 8 6 9 25 26 20 8 34 30 35 17 30 21 26 29 27 57 58 51 62 57 76 65 76 104 87 99 108 112 117 127 174 147 155 166 185 213 208 206 238 224 255 232 232 255 255 254 255 255 255 255 255 255 255 255 255 255 226 215 235 238 211 172 208 188 181 151 143 129 132 116 119 112 93 96 99 66 68 53 65 43 64 30 51 26 33 41 23 25 15 25 27 23 24 26 20 11 10 23 17 10 4 14 23 20 2 25 3 14 11]; % in uint8
Daten_normiert = Daten ./ sum(Daten);
ydata = double(Daten_normiert);
xdata = 1:length(Daten_normiert);
plot(xdata,ydata);
hold on
mu = sum(Daten.*xdata)/sum(Daten)
sig = 20; % geschätzt;
x=[mu sig];
F=lsqcurvefit(@Gauss,x,xdata,Daten_normiert)
yFitted = Gauss(F, xdata);
plot(xdata, yFitted)
hold off

Funktion ohne Link?

Grüße,
Harald
_________________

1.) Ask MATLAB Documentation
2.) Search gomatlab.de, google.de or MATLAB Answers
3.) Ask Technical Support of MathWorks
4.) Go mad, your problem is unsolvable ;)

SaFW

Themenstarter

Forum-Anfänger


	Beiträge: 12

	Anmeldedatum: 24.02.20

	Wohnort: ---

	Version: ---

Verfasst am: 23.03.2020, 19:00 Titel:

Hallo,

ich bedanke mich sehr für deine Hilfe! Very Happy

Was ich noch nicht ganz verstehe ist, warum das Sigma jetzt geschätzt wird, wenn man doch den std Befehl hat? Hat bestimmt was mit der Normierung zu tun, wäre aber fürs Verständnis gut zu wissen.
Und wäre es noch irgendwie möglich gewesen es anders herum zu machen? Also, dass ich meine gefitteten Daten an meine ursprüngliche Datenkurve anpasse, anstatt die Kurve zu normieren? Da hab ich mich nämlich eher drauf konzentriert und bin auf keinen vernünftigen Gedanken gekommen Confused

Gruß

Harald

Forum-Meister


	Beiträge: 24.495

	Anmeldedatum: 26.03.09

	Wohnort: Nähe München

	Version: ab 2017b

Verfasst am: 23.03.2020, 19:15 Titel:

Hallo,

weil nicht die std von den y-Werten genommen werden müsste, sondern von den x-Daten in der Häufigkeit der y-Werte. Das Auszuklambüstern war mir dann doch zu mühsam.

Ob du jetzt die Daten durch sum(Daten) teilst oder die Kurve mit sum(Daten) multiplizierst, ist gleichgültig.

Grüße,
Harald
_________________

1.) Ask MATLAB Documentation
2.) Search gomatlab.de, google.de or MATLAB Answers
3.) Ask Technical Support of MathWorks
4.) Go mad, your problem is unsolvable ;)

SaFW

Themenstarter

Forum-Anfänger


	Beiträge: 12

	Anmeldedatum: 24.02.20

	Wohnort: ---

	Version: ---

Verfasst am: 25.03.2020, 19:34 Titel:

Hallo,

was meinst du jetzt genau mit

Zitat:

von den x-Daten in der Häufigkeit der y-Werte

?
Ist damit eine Häufigkeitsdichte gemeint?

Trotzdem hätte ich das wohl ohne deine Hilfe nie hinbekommen und daher danke ich dir sehr! Very Happy

Grüße

Harald

Forum-Meister


	Beiträge: 24.495

	Anmeldedatum: 26.03.09

	Wohnort: Nähe München

	Version: ab 2017b

Verfasst am: 25.03.2020, 21:24 Titel:

Hallo,

ich meinte das so... man kann Daten so interpretieren, dass...
1 3 mal vorkam
2 24 mal vorkam
3 4 mal vorkam
etc.

d.h. der Mittelwert und auch die Standardabweichung müssen von 1, 2, 3 etc. in der Gewichtung von Daten genommen werden.

Grüße,
Harald
_________________

1.) Ask MATLAB Documentation
2.) Search gomatlab.de, google.de or MATLAB Answers
3.) Ask Technical Support of MathWorks
4.) Go mad, your problem is unsolvable ;)

SaFW

Themenstarter

Forum-Anfänger


	Beiträge: 12

	Anmeldedatum: 24.02.20

	Wohnort: ---

	Version: ---

Verfasst am: 26.03.2020, 20:14 Titel:

Hallo,

ah okay dankeschön. Das ist verständlich Very Happy

Das eigentliche Ziel des fittens wurde ja erreicht. Deswegen würde ich das als beantwortet betrachten und mich nochmals sehr für deine Hilfe bedanken! Smile

Für alle, die zukünftig auch auf so ein Problem stoßen ist hier nochmal der Code, bei dem sich die Fitkurve hochskaliert und an die Originaldaten anpasst. Die Gaussfunktion blieb ja dann unverändert, somit brauch ich die nicht nochmal mit hin schreiben.

Code:

Daten= [3 24 4 11 18 6 12 7 16 3 28 8 6 9 25 26 20 8 34 30 35 17 30 21 26 29 27 57 58 51 62 57 76 65 76 104 87 99 108 112 117 127 174 147 155 166 185 213 208 206 238 224 255 232 232 255 255 254 255 255 255 255 255 255 255 255 255 255 226 215 235 238 211 172 208 188 181 151 143 129 132 116 119 112 93 96 99 66 68 53 65 43 64 30 51 26 33 41 23 25 15 25 27 23 24 26 20 11 10 23 17 10 4 14 23 20 2 25 3 14 11]; % in uint8
Daten_normiert = Daten ./ sum(Daten);
ydata = double(Daten);
xdata = 1:length(ydata);
plot(xdata,ydata);
hold on
mu = sum(Daten.*xdata)/sum(Daten)
sig = 20; % geschätzt
x=[mu sig];
F=lsqcurvefit(@Gauss,x,xdata,Daten_normiert)
yFitted = Gauss(F, xdata).*sum(Daten);
plot(xdata, yFitted);
hold off

Funktion ohne Link?

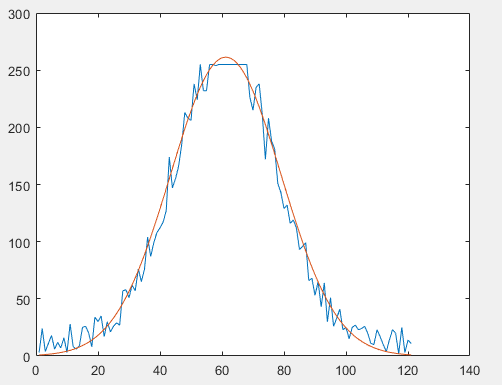
Grüße,
David

Jonathan

Gast


	Beiträge: ---

	Anmeldedatum: ---

	Wohnort: ---

	Version: ---

Verfasst am: 26.03.2020, 23:46 Titel:

Hallo, ich hab ungefähr das selbe problem mit dem fitt, bloß gibt es bei mir vorgegebene x-werte. Hab versucht den code soweit zu übernehmen um zu gucken ob es funktioniert. Hat aber nicht so wirklich :/

Funktion:

Code:

function G= myfun(x,ydata)
mu = x(1);
sig = x(2);
G=-(1/(sig*(sqrt(2*pi)))*exp(((-1/2)*((ydata-mu)/sig).^2)));
end

Funktion ohne Link?

hab die Funktion negiert,weil ich mir dachte dass meine Daten ja auch negativ verlaufen

Code:

Code:

Daten=[1010 1000 980 950 910 850 780 710 640 580 510 490 490 490 530 570 650 710 790 850 900 950 970 1000 1010];
xwerte=[-3000 -2750 -2500 -2250 -2000 -1750 -1500 -1250 -1000 -750 -500 -250 0 250 500 750 1000 1250 1500 1750 2000 2250 2500 2750 3000];
Daten_normiert = Daten ./ sum(Daten);
ydata = double(Daten);
xdata = xwerte;
p1=plot(xdata,ydata,'b.');
hold on
mu = sum(Daten.*xdata)/sum(Daten)
sig = 20;
x=[mu sig];
F=lsqcurvefit(@gauss,x,xdata,Daten_normiert)
yFitted = gauss(F, xdata).*sum(Daten);
p2=plot(xdata, yFitted,'g');
p2.LineWidth=2;
hold off

Funktion ohne Link?

Das Ergebnis sieht so aus

Hat denke ich auch was mit der Skalierung zu tun. Weiß aber nicht was genau. Hab rumprobiert, dadurch wurde es aber nicht besser.
Hoffe man kann auch mir Matlab deppen helfen Embarassed

Gruß
Jonathan

Harald

Forum-Meister


	Beiträge: 24.495

	Anmeldedatum: 26.03.09

	Wohnort: Nähe München

	Version: ab 2017b

Verfasst am: 27.03.2020, 09:47 Titel:

Hallo,

Zitat:

hab die Funktion negiert,weil ich mir dachte dass meine Daten ja auch negativ verlaufen

Das ist ein Gedanke in die richtige Richtung, aber nicht weit genug. Deine Werte sind ja nun nicht negativ, sondern verlaufen von 1010 aus nach unten. D.h. gute Ansätze wären
f = 1010 - Gauss
oder
f = c - Gauss mit zu bestimmendem c (würde zu x(3) )

Zudem wurde in dem Code ja sigma = 20 geschätzt. Wenn man andere Daten hat, muss man auch anders schätzen. Ich würde bei dem Datensatz eher 1000-1500 schätzen.

Grüße,
Harald
_________________

1.) Ask MATLAB Documentation
2.) Search gomatlab.de, google.de or MATLAB Answers
3.) Ask Technical Support of MathWorks
4.) Go mad, your problem is unsolvable ;)

Busmaster

Forum-Anfänger


	Beiträge: 18

	Anmeldedatum: 05.08.09

	Wohnort: Dresden

	Version: Matlab2014, Matlab Online, Octave

Verfasst am: 27.03.2020, 12:03 Titel:

Hallo,
es geht hier ja offenbar um Anpassen von Messwerten an eine Gauss-förmige Funktion (nicht strenggenommen um eine Wahrscheinlichkeitsdichte), da Maximum < 0 und Offset möglich sind.

Dazu verwende ich die Funktion gauss2.m
Dort taucht die Amplitude explizit auf; das erleichtert das Schätzen des Startwertes.

Ergebnis des Lsqfits
mu = -3.91925; % gefundene Lage des Maximums/Minimums der Gauss-Funktion
sig = 1186.73972; % gefundene Breite
mgauss = -560.6591; % gefundenes Maximum/Minimum der Gauss-Funktion
offset = 1037.42384; % gefundenes Offset

Gruss
Busmaster

Code:

% Beispiel mit Octave

clear
Daten=[1010 1000 980 950 910 850 780 710 640 580 510 490 490 490 530 570 650 710 790 850 900 950 970 1000 1010];
xwerte=[-3000 -2750 -2500 -2250 -2000 -1750 -1500 -1250 -1000 -750 -500 -250 0 250 500 750 1000 1250 1500 1750 2000 2250 2500 2750 3000];

ydata = double(Daten);
xdata = xwerte;

p1 = plot(xdata,ydata,'bo');
grid
hold on

% allg. Gauss-Funktion G = mgauss * exp(((-1/2)*((ydata-mu)/sig).^2)) + offset;
% Schätzung
mu = 0; % geschätzte Lage des Maximums/Minimums der Gauss-Funktion
sig = 1500; % geschätzte Breite
mgauss = -500; % geschätztes Maximum/Minimum der Gauss-Funktion
offset = 1000; % geschätztes Offset

x = [mu sig mgauss offset]; % Vektor der Parameter zur Übergabe an Gauss2

F = lsqcurvefit(@gauss2,x,xdata,ydata)

yFitted = gauss2(F, xdata);

p2=plot(xdata, yFitted,'r');

hold off

function G = gauss2(x,ydata)
% Allgemeine Gauss-Funktion mit Offset

mu = x(1); % Lage des Maximums/Minimums der Gauss-Funktion
sig = x(2); % Breite der Gauss-Funktion
mgauss = x(3); % Maximum/Minimum der Gauss-Funktion
offset = x(4); % Offset

G = mgauss * exp(((-1/2)*((ydata-mu)/sig).^2)) + offset;

end

Funktion ohne Link?

lsqfit.png

Beschreibung:

Download

Dateiname:

lsqfit.png

Dateigröße:

26.03 KB

Heruntergeladen:

228 mal

Jonathan

Gast


	Beiträge: ---

	Anmeldedatum: ---

	Wohnort: ---

	Version: ---

Verfasst am: 27.03.2020, 15:02 Titel:

Hallo,

ja genau das war das Ziel! Dankeschön für die schnelle Hilfe! Smile

Gruß
Jonathan

	Gehe zu Seite Zurück 1, 2
Einstellungen und Berechtigungen
Beiträge der letzten Zeit anzeigen:	Du kannst Beiträge in dieses Forum schreiben. Du kannst auf Beiträge in diesem Forum antworten. Du kannst deine Beiträge in diesem Forum nicht bearbeiten. Du kannst deine Beiträge in diesem Forum nicht löschen. Du kannst an Umfragen in diesem Forum nicht mitmachen. Du kannst Dateien in diesem Forum posten Du kannst Dateien in diesem Forum herunterladen

Impressum | Nutzungsbedingungen | Datenschutz | FAQ |

RSS

Hosted by:

Copyright © 2007 - 2025 goMatlab.de | Dies ist keine offizielle Website der Firma The Mathworks

MATLAB, Simulink, Stateflow, Handle Graphics, Real-Time Workshop, SimBiology, SimHydraulics, SimEvents, and xPC TargetBox are registered trademarks and The MathWorks, the L-shaped membrane logo, and Embedded MATLAB are trademarks of The MathWorks, Inc.