Einheit der Amplitude im Frequenzspektrum

WICHTIG: Der Betrieb von goMatlab.de wird privat finanziert fortgesetzt. - Mehr Infos...

Partner:

Forum

Option

[Erweitert]

• Diese Seite per Mail weiterempfehlen

Gehe zu:

tek88

Gast


	Beiträge: ---

	Anmeldedatum: ---

	Wohnort: ---

	Version: ---

Verfasst am: 09.06.2013, 14:25 Titel: Einheit der Amplitude im Frequenzspektrum

Hallo,
ich habe schon einige Forumsbeiträge durchgelesen wo es um ähnliches ging, jedoch weiss ich noch immer nicht mehr.
Ich hab ein Signal mit Beschleunigungswerten [m/s^2] mit 100 Hz aufgenommen und im Zeitbereich geplotted. Weiter habe ich das ganze Fourier-transformiert mit folgendem Code:

Code:

NFFT = 2^nextpow2(L); % Next power of 2 from length of y
AX = fft(Ax,NFFT)/L; % fft of accelerations Ax
f1 = Fs/2*linspace(0,1,NFFT/2+1);

plot(f1,2*abs(AX(1:NFFT/2+1)),'r') % plot of the fft
hold on
title('Fourier-transformed Signal')
xlabel('Frequency (Hz)')
ylabel('|Y(f)|')
legend

Funktion ohne Link?

Nun meine Frage. Was für Einheiten ergibt mir diese Fourier Transformation für die Amplituden im Frequenzspektrum?
Ich weiss das es entweder mit "Amplitude" oder "Power" umschrieben wird, jedoch wie ist da der Zusammenhang zum Ausgangssignal, resp. den m/s^2?
Vielen Dank für eure Hilfe!

Balzer82

Forum-Anfänger


	Beiträge: 26

	Anmeldedatum: 22.02.11

	Wohnort: Dresden

	Version: ---

Verfasst am: 12.12.2013, 09:06 Titel:

Wenn du den Betrag korrekt dargestellt hast (gibt verschiedene Arten), dann ist es auch m/s2, denn es ist ja der Betrag der Amplitude.

Vielleicht hilft dir schon diese Animation:

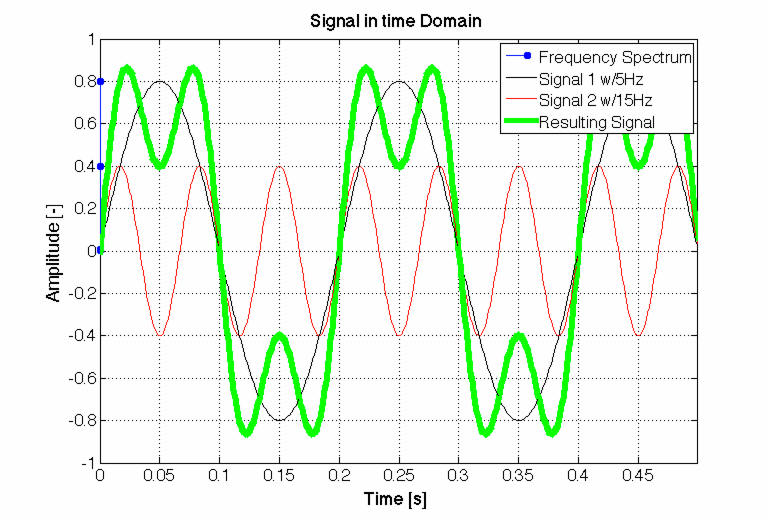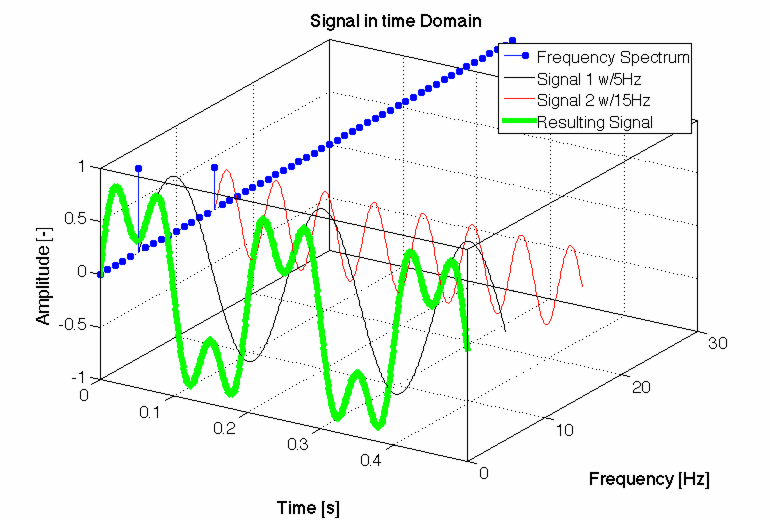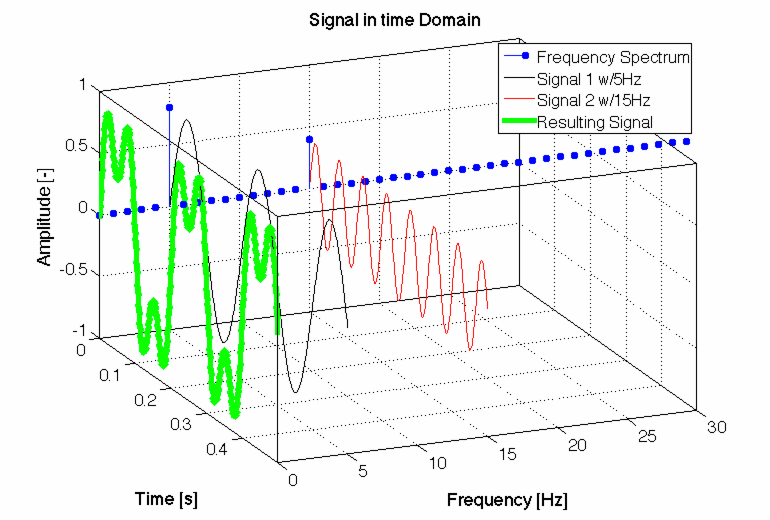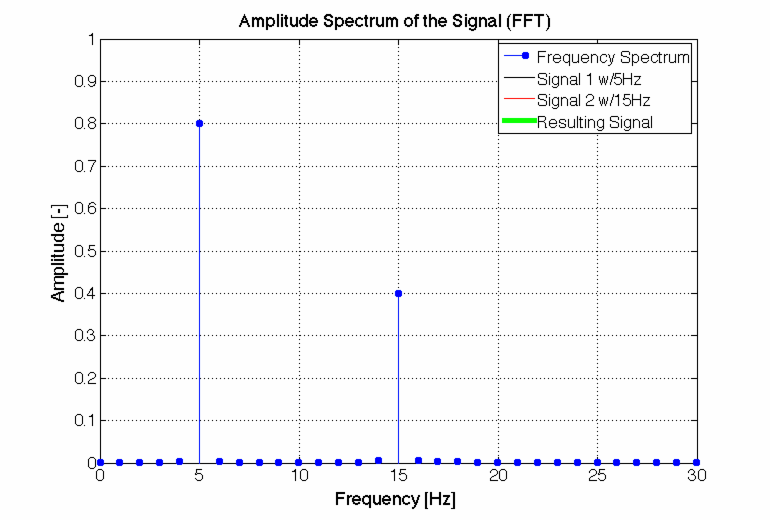
Oft wird es in db angegeben und bezieht sich auf eine "Referenzgröße", ist dann also Einheitenlos bzw. in db angegeben. Bei einer Beschleunigung aber wohl eher nicht.
_________________

"Bremsen ist die sinnlose Umwandlung von Exergie in Anergie - daran kann man sich höchstens noch die Finger verbrennen" - Prof. J. Morgenstern

Napomleb

Forum-Anfänger


	Beiträge: 30

	Anmeldedatum: 27.08.13

	Wohnort: ---

	Version: ---

Verfasst am: 13.12.2013, 11:30 Titel:

Hallo,

noch als kleine Ergänzung zur coolen Grafik.

Hinter der Fouriertransformation steckt doch mathematisch das Integral.
Wenn ich meine Beschleunigung $\frac{m}{s^{2} }$ transformier (bzw integrier), würde ich daraus eine Geschwindigkeit $\frac{m}{s}$ erhalten.

Jetzt muss aber beachtet werden, ob es sich um eine kontinuierliche oder diskrete Transformation handelt Wink

Gibt also keine pauschaule Aussage, welche Einheit angegeben wird.

Sehr hilfreich dazu: http://www.uni-protokolle.de/foren/viewt/273229,0.html

Viele Grüße


Einstellungen und Berechtigungen
Beiträge der letzten Zeit anzeigen:	Du kannst Beiträge in dieses Forum schreiben. Du kannst auf Beiträge in diesem Forum antworten. Du kannst deine Beiträge in diesem Forum nicht bearbeiten. Du kannst deine Beiträge in diesem Forum nicht löschen. Du kannst an Umfragen in diesem Forum nicht mitmachen. Du kannst Dateien in diesem Forum posten Du kannst Dateien in diesem Forum herunterladen

Impressum | Nutzungsbedingungen | Datenschutz | FAQ |

RSS

Hosted by:

Copyright © 2007 - 2024 goMatlab.de | Dies ist keine offizielle Website der Firma The Mathworks

MATLAB, Simulink, Stateflow, Handle Graphics, Real-Time Workshop, SimBiology, SimHydraulics, SimEvents, and xPC TargetBox are registered trademarks and The MathWorks, the L-shaped membrane logo, and Embedded MATLAB are trademarks of The MathWorks, Inc.