|
|
|
Luftstrommischer Differentialgleichung , Zustandsraummodell |
|
| chr1stoph |
Forum-Newbie
|
 |
Beiträge: 1
|
|
|
|
Anmeldedatum: 26.06.18
|
|
|
|
Wohnort: ---
|
|
|
|
Version: ---
|
|
|
|
 |
|
Verfasst am: 26.06.2018, 09:33
Titel: Luftstrommischer Differentialgleichung , Zustandsraummodell
|
 |
Hi Leute,
ich habe für mein Praktikum eine Aufgabe eines vereinfachten Luftstrommischers zu lösen.
Ein warmer und ein kalter Luftstrom ( es werden gleiche Dichte und perfektes Mischen vorausgesetzt)
sollen so gemischt werden das eine konstante Wunschtemperatur und konstantes Wunschvolumen am Ausgang vorhanden sind. Die regelbaren Größen sind die zwei Volumina V1 und V2.
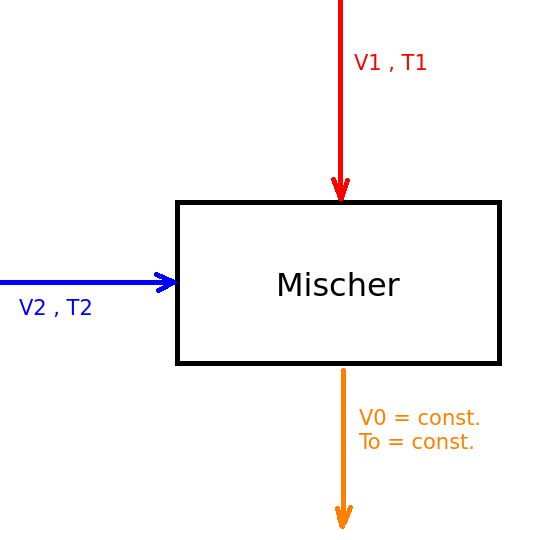
Mein Ansatz war über die Richmansche Mischungsregel
sowie 
aber ich schaffe es nicht auf eine Differentialgleichung zu kommen und somit nicht auf ein Zustandsraummodell in Matrizenform um einen Regler zu entwickeln.
Kann mir jemand helfen oder einen Tipp geben ?
Ganz lieben Dank,
Christoph
|
|
|
|
|
|
| Epfi |
Forum-Meister
|
|
Beiträge: 1.134
|
|
|
|
Anmeldedatum: 08.01.09
|
|
|
|
Wohnort: ---
|
|
|
|
Version: ---
|
|
|
|
|
|
|
Verfasst am: 26.06.2018, 18:25
Titel:
|
|
Wenn Dein Ansatz keine Ableitungen/Integrationen enthält, hast Du halt einfach keine Differenzialgleichung. Oder anders gesagt: Deine Ausgangsgrößen hängen nur von den aktuellen Eingangsgrößen ab und nicht von irgendwelchen vorher herrschenden Werten.
Kannst Du Deine Gleichungen so ineinander einsetzen und auflösen, dass Du je eine Gleichung für V1 und V2 bekommst? Falls ja:
Wenn V1 nicht von V2 abhängt oder V2 nicht von V1 abhängt, kannst Du die Größen einfach so ausrechnen, damit Deine Randbedingungen erfüllt sind.
Wenn V1 und V2 in Deinen Gleichungen immer voneinander abhängig sind, wirst Du wahrscheinlich nicht drumherum kommen, mit einem numerischen Lösungsverfahren eine Lösung für Dein Gleichungssystem zu finden.
|
|
|
|
|
|
|
Einstellungen und Berechtigungen
|
|
Du kannst Beiträge in dieses Forum schreiben.
Du kannst auf Beiträge in diesem Forum antworten.
Du kannst deine Beiträge in diesem Forum nicht bearbeiten.
Du kannst deine Beiträge in diesem Forum nicht löschen.
Du kannst an Umfragen in diesem Forum nicht mitmachen.
Du kannst Dateien in diesem Forum posten
Du kannst Dateien in diesem Forum herunterladen
|
|
Impressum
| Nutzungsbedingungen
| Datenschutz
| FAQ
|  RSS
Hosted by:
Copyright © 2007 - 2024
goMatlab.de | Dies ist keine offizielle Website der Firma The Mathworks
MATLAB, Simulink, Stateflow, Handle Graphics, Real-Time Workshop, SimBiology, SimHydraulics, SimEvents, and xPC TargetBox are registered trademarks and The MathWorks, the L-shaped membrane logo, and Embedded MATLAB are trademarks of The MathWorks, Inc.
|
|
