|
|
|
Masse Feder Dämpfer System |
|
| hegi |
Forum-Newbie
|
 |
Beiträge: 6
|
|
|
|
Anmeldedatum: 03.07.11
|
|
|
|
Wohnort: ---
|
|
|
|
Version: ---
|
|
|
|
 |
|
Verfasst am: 10.07.2011, 12:34
Titel: Masse Feder Dämpfer System
|
 |
Hallo,
könnte mir vlt jemand die Differential Gleichung für folgendes AWP Problem aufstellen ?
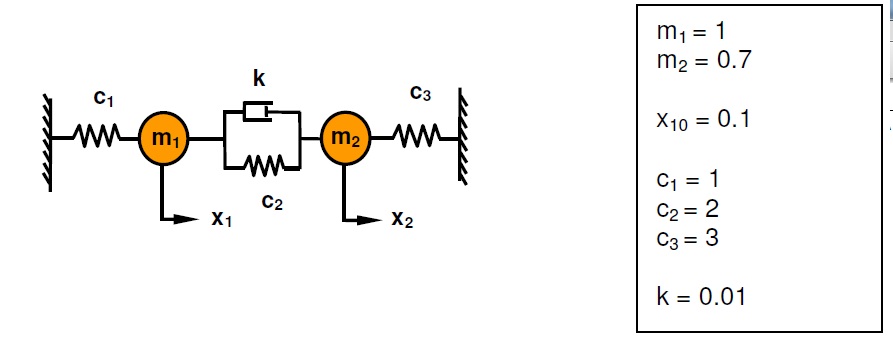
gruß und vielen dank im voraus
| Beschreibung: |
|
Download |
| Dateiname: |
bild2.jpg |
| Dateigröße: |
43.47 KB |
| Heruntergeladen: |
2726 mal |
|
|
|
|
|
|
| Georg J |
Forum-Century
|
|
Beiträge: 113
|
|
|
|
Anmeldedatum: 22.06.11
|
|
|
|
Wohnort: ---
|
|
|
|
Version: R2008a
|
|
|
|
|
|
|
Verfasst am: 11.07.2011, 21:54
Titel:
|
|
| |
 |
 |
Hi Hegi,
Gibt es da eine kleine Hausaufgabe zu lösen?
Das sollte doch eigentlich nicht so schwierig sein. Am besten zuerst die Massen frei machen und das Kräftegleichgewicht für beide Massen notieren. Dann die charakteristischen Gleichungen für die Feder- und Dämpferkräfte aufstellen Fc = c*(x_rechts - x_links) bzw Fd = k*(dx_rechts- dx_links) und einfügen. Fertig!
Die DG lauten:
m1*ddx1 - k(dx2-dx1) + c1x1 - c2(x2-x1) = 0
m2*ddx2+ k(dx2-dx1) + c2(x2-x1) + c3x2 = 0
ddx = 2. Ableitung von x nach der Zeit
dx = 1. Ableitung von x nach der Zeit
Ich hab es in ein State-Space Modell umgeschrieben und die Eigenfrequenzen berechnet. Ausserdem hab ich das AWP gelöst, weil ich sehen wollte, wie es schwingt.
Es ist ein schwach gedämpftes System und es gibt schöne Phasenportraits 
Gruss, Georg
| Beschreibung: |
|
Download |
| Dateiname: |
two_mass_main.m |
| Dateigröße: |
963 Bytes |
| Heruntergeladen: |
2157 mal |
| Beschreibung: |
| Funktion mit Differentialgleichung für ODE Solver |
|
Download |
| Dateiname: |
two_mass.m |
| Dateigröße: |
146 Bytes |
| Heruntergeladen: |
1865 mal |
|
|
|
|
| Jan S |
Moderator
|
|
Beiträge: 11.057
|
|
|
|
Anmeldedatum: 08.07.10
|
|
|
|
Wohnort: Heidelberg
|
|
|
|
Version: 2009a, 2016b
|
|
|
|
|
|
|
Verfasst am: 12.07.2011, 01:51
Titel:
|
|
Hallo Georg J,
| Zitat: |
| Gibt es da eine kleine Hausaufgabe zu lösen? |
Was bleibt Hegi nun noch zu tun? Er muss bei der Abgabe der Aufgabe natürlich mitteilen, dass er im Forum Hilfe bekommen hat. Ich würde ihm die Lösung sonst als Übungsgruppenleiter nicht anerkennen, man könnte auch sagen "um die Ohren hauen".
Gruß, Jan
|
|
|
|
| Georg J |
Forum-Century
|
|
Beiträge: 113
|
|
|
|
Anmeldedatum: 22.06.11
|
|
|
|
Wohnort: ---
|
|
|
|
Version: R2008a
|
|
|
|
|
|
|
Verfasst am: 12.07.2011, 23:14
Titel:
|
|
Hi Jan,
Klar hast du recht und ich hab Hegi alles gelöst. Aber mich hat einfach das Interesse gepackt 
Mir ist es egal, was er mit meiner Lösung macht. Wenn er sie einfach abgibt und sich selbst keine Gedanken dazu macht, lernt er halt nichts.
Jeder ist seines eigenen Glückes Schmied 
Gruss, Georg
|
|
|
|
| Xamb |
Gast
|
|
Beiträge: ---
|
|
|
|
Anmeldedatum: ---
|
|
|
|
Wohnort: ---
|
|
|
|
Version: ---
|
|
|
|
|
|
|
Verfasst am: 25.08.2011, 16:33
Titel: Ähnliches Problem
|
|
| |
|
|
Hi,
ich sitze gerade vor einem ähnlichen Problem. Ich soll mit MatLab ein N-Feder-Massen-Dämpfer System simulieren (siehe Bild), d.h. Eigenfrequenzen bestimmen. Anschließend soll eine beliebige Masse mi zusätzlich eine harmonische Schwingung (u(t)=Fcos(Ot)) induzieren.
Allerdings bin kein Mechaniker und auch in MatLab nicht so sehr bewandert. Von daher mein Frage hier: Wie mach ich das?
Also die DGLs dazu habe ich schon aufgestellt:
m1*ddx1 + c1(x1-x0) - c2(x2-x1) - b1(dx1-dx0) + b2(dx2-dx1) = 0
...
...
mi*ddxi + ci(xi-xi-1) - ci+1(xi+1-xi) - bi(dxi-dxi-1) + bi+1(dxi+1-dxi) = 0
...
mn*ddxn + cn(xn-xn-1)
wobei x0 = dx0 = 0 ist da links an der wand befestigt. Zur Notation hier im Forum: xi-1 = x_(i-1), d.h. das -1 bzw +1 bezeiht sich auf den Index, hoffe das ist verständlich 
Naja, im wesentlichen ergeben sich daraus die Matrizen M, C und B. Wobei M eine Diagonalmatrix mit den Massen, C die Matrix der aus den DGLn resultierenden Federkonstanten und B die entsprechend resultierende Dämpfungsmatrix ist. Soweit sogut...
Also: Mddx + Bdx + Cx = f'
(mit f' zunächst Null Vektor - stationäre Lösung, anschließend mit fi=u(t)).
Was muss ich nun tut um die Eigenfrequenzen des Systems zu bestimmen? Was sind die Frequenzgang-Funktionen dazu, bzw. wie bekomme ich diese heraus, das wäre sehr nice...
Ich würde mich sehr freun, falls mir einer von euch weiterhelfen könnte, stehe nämlich zur Zeit ziemlich auf dem Schlauch, schon mal vielen Dank vor ab,
Gruß Xam
| Beschreibung: |
|
Download |
| Dateiname: |
Schwinger.png |
| Dateigröße: |
37.99 KB |
| Heruntergeladen: |
2940 mal |
|
|
|
|
| Georg J |
Forum-Century
|
|
Beiträge: 113
|
|
|
|
Anmeldedatum: 22.06.11
|
|
|
|
Wohnort: ---
|
|
|
|
Version: R2008a
|
|
|
|
|
|
|
Verfasst am: 26.08.2011, 20:42
Titel:
|
|
Hi Xam,
Ich habe gerade keine Zeit ausführlich zu schreiben, aber du kannst dein System mit der Funktion sys erstellen und mit step simulieren. Du kannst dir mit bode auch den Bodeplot dazu anzeigen lassen.
Suche doch mal in der Hilfe nach diesen Funktionen.
Gruss, Georg
|
|
|
|
|
|
Verfasst am: 30.05.2019, 13:22
Titel:
|
|
Hallo Xamb,
hast du das Problem lösen können? Wenn ja, könntest du mir den Code schicken? Ich muss ein ähnliches Problem lösen mit 3 Massen.
|
|
|
|
|
|
|
Einstellungen und Berechtigungen
|
|
Du kannst Beiträge in dieses Forum schreiben.
Du kannst auf Beiträge in diesem Forum antworten.
Du kannst deine Beiträge in diesem Forum nicht bearbeiten.
Du kannst deine Beiträge in diesem Forum nicht löschen.
Du kannst an Umfragen in diesem Forum nicht mitmachen.
Du kannst Dateien in diesem Forum posten
Du kannst Dateien in diesem Forum herunterladen
|
|
Impressum
| Nutzungsbedingungen
| Datenschutz
| FAQ
|  RSS
Hosted by:
Copyright © 2007 - 2024
goMatlab.de | Dies ist keine offizielle Website der Firma The Mathworks
MATLAB, Simulink, Stateflow, Handle Graphics, Real-Time Workshop, SimBiology, SimHydraulics, SimEvents, and xPC TargetBox are registered trademarks and The MathWorks, the L-shaped membrane logo, and Embedded MATLAB are trademarks of The MathWorks, Inc.
|
|
